Konstruktionen spezieller Kurvenpaare und deren
Untersuchung mit Mathematica
Zusammenfassung der Diplomarbeit von Alexandra Moese
Sommersemester 2001
 Aus jeder regulären Kurve
Aus jeder regulären Kurve 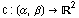 kann man durch verschiedene allgemeine Konstruktionen neue erzeugen.
kann man durch verschiedene allgemeine Konstruktionen neue erzeugen.
Diese Konstruktionen können als Funktionen angesehen werden, die
mit den Ursprungsfunktionen Kurvenpaare bilden. Diese Kurvenpaare wollen
wir näher untersuchen.
In dieser Arbeit stellen wir sieben verschiedene Konstruktionen vor und
wenden diese auf die Kegelschnitte sowie einige Rollkurven an. Die dabei
entstandenen Kurven sind in zwei Tabellen am Ende
dieser Seite aufgelistet.
Im folgenden bezeichnen T, N den Einheitstangenten bzw. Normalenvektor der Kurve c,
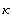 die Krümmung und
die Krümmung und 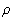 den Krümmungsradius. den Krümmungsradius.
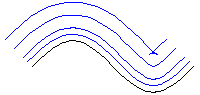
Parallelkurven
Parallelkurven sind Kurven, die einen
festen Abstand k zu einer regulären Kurve c einhalten.
Sie sind durch die Gleichung
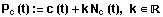
definiert.
Für t0 mit 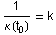 ist die Parallelkurve nicht regulär.
ist die Parallelkurve nicht regulär. |
|
Fußpunktkurven
|
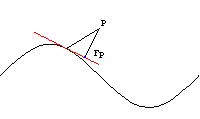
Die Menge der Fußpunkte Fp der Lote von einem festen
Punkt P auf die Tangente an die Kurve c heißt
Fußpunktkurve.
Die Fußpunktkurve einer regulären Kurve c in
Bezug auf den festen Punkt P ist durch eine Gleichung der
Form
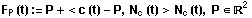
gegeben.
Ist die Krümmung von c gleich Null oder liegt der
feste Punkt P auf der Kurve, erhalten wir nichtreguläre
Fußpunktkurven.
|
|
Evolute
Die Evolute ist der geometrische Ort
der Mittelpunkte der Schmiegkreise an die reguläre Kurve c.
Des weiteren ist die Evolute die Hüllkurve der Kurvenschar
der Normalen an c. Aufgrund dieser Tatsache ist der Tangentenvektor
von 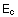 parallel zu dem Normalenvektor von c. Denselben Zusammenhang
können wir für den Normalenvektor von
parallel zu dem Normalenvektor von c. Denselben Zusammenhang
können wir für den Normalenvektor von 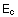 und den Tangentenvektor von c aufstellen.
und den Tangentenvektor von c aufstellen.
Wir definieren die Evolute durch die Gleichung:
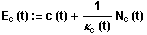
Die Evolute der Kurve c ist dann nicht regulär, wenn
die Krümmung von c konstant ist bzw. in den kritischen
Punkten der Krümmung. |
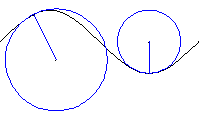
|
|
Involute
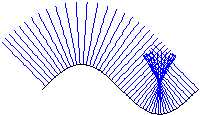
Die Involute stellt die ''Umkehrung'' der Evolute
dar. Geometrisch läßt sich die Involute als Abwicklung
eines um die reguläre Kurve c straff gespannten Fadens
beschreiben.
Die Involte zur Konstanten k ist durch
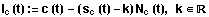
gegeben.
Gilt 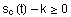 ,
so kann ,
so kann 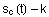 als
Länge des Fadens interpretiert werden. Für als
Länge des Fadens interpretiert werden. Für 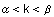 sagt man, die Abwicklung beginnt in c(k) .
sagt man, die Abwicklung beginnt in c(k) .
Zu jeder beliebigen Konstante k ergibt die Evolute der Involute
von c wieder die Ursprungskurve c. Die Involute der
Evolute von c liefert jedoch nur zur Konstanten 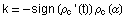 die Ursprungskurve c. Der Krümmungsradius der Involute
spiegelt die Fadenlänge wieder und der Tangentenvektor von
die Ursprungskurve c. Der Krümmungsradius der Involute
spiegelt die Fadenlänge wieder und der Tangentenvektor von
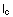 ist parallel zum Normalenvektor von c und der Normalenvektor
von
ist parallel zum Normalenvektor von c und der Normalenvektor
von 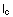 parallel zum Tangentenvektor von c. Die Involuten zu verschiedenen
Konstanten k sind Parallelkurven.
parallel zum Tangentenvektor von c. Die Involuten zu verschiedenen
Konstanten k sind Parallelkurven.
Eine Involute ist in den Stellen nicht regulär, in denen 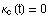 gilt. Des weiteren ist eine Involute für
gilt. Des weiteren ist eine Involute für 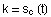 nicht regulär, also in dem Punkt, in dem c die Involute
nicht regulär, also in dem Punkt, in dem c die Involute
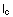 berührt.
berührt. |
Katakaustik zu parallelem Licht
Fällt paralleles Licht auf die
Kurve c und wird an ihr reflektiert, so bildet die Hüllkurve
der Reflexionen die Katakaustik zu parallelem Licht der regulären
Kurve c.
Diese Katakaustik wird durch die Gleichung
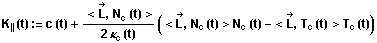
mit 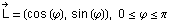 als Lichtrichtung der einfallenen Strahlen beschrieben.
als Lichtrichtung der einfallenen Strahlen beschrieben.
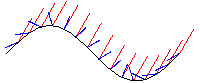
Aufgrund ihrer Entstehung als Hüllkurve ist der Tangentenvektor
der Katakaustik parallel zu dem Reflexionsvektor. |
|
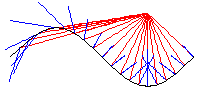
Katakaustik zu punktförmigem Licht
|
Im Unterschied zu der Katakaustik zu parallelem Licht fällt
bei dieser Konstruktion punktförmiges Licht auf die Kurve
c und wird reflektiert.
Auch hier bildet die Hüllkurve der Reflexionen die Katakaustik,
die durch die Gleichung
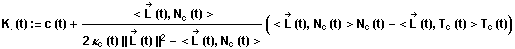
gegeben ist.
|
|
Radienkurven
In dieser Konstruktion betrachten wir
den durch 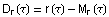 gebildeten Vektor, also den Radienvektor vom Mittelpunkt
gebildeten Vektor, also den Radienvektor vom Mittelpunkt 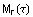 des rollenden Kreises r zu dem betrachteten Punkt, der die
Rollkurve
des rollenden Kreises r zu dem betrachteten Punkt, der die
Rollkurve 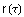 beschreibt.
beschreibt.
Die Hüllkurve der durch
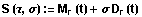
beschriebenen Kurvenschar bezeichnen wir als Radienkurve. Diese
ist jedoch stark von der jeweiligen Rollkurve abhängig, so
daß keine allgemeine Gleichung aufgestellt werden kann.
Betrachtet man s als Scharparameter und nicht als Kurvenparameter,
so erhält man wieder die allgemeine Gleichung einer Rollkurve. |

|
|