Kurven im Raum
Vergleich von verschiedenen begleitenden Dreibeinen
Zusammenfassung der Diplomarbeit von Gordana Skoric-Knabe SS 1997
1. Prüfer:
Prof. Dr. Angela Schwenk-Schellschmidt
2. Prüfer:
Prof. Dr. Martin Ochmann
Bei der Untersuchung von gekrümmten Linien versagt die Elementargeometrie, obwohl die Natur und Wissenschaft voll von Kurven und Flächen verschiedenster Gestalt ist. Diesen Mangel versucht die Differentialgeometrie auszugleichen.
Um verschiedenste Raumkurven zu untersuchen, ist es vom Vorteil, in jedem Punkt der Kurve ein Koordinatensystem einzuführen. Ein solches Koordinatensystem wird auch begleitendes Dreibein genannt. Die Idee mit dem sich entlang einer Kurve bewegenden Koordinatensystem stammt aus der Mechanik (1736 L.Euler).
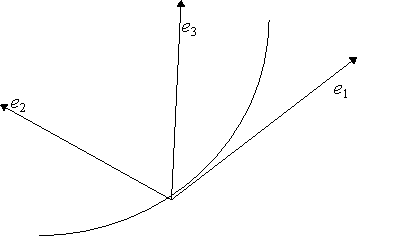
Ein begleitendes Dreibein einer Raumkurve besteht in jedem Punkt der Kurve aus drei Einheitsvektoren, die paarweise senkrecht aufeinander stehen, wie im folgenden Bild dargestellt ist.

Zu einer Raumkurve existieren viele verschiedene begleitende Dreibeine, die sich durch ihre Lage im Raum unterscheiden. Es ist möglich, ein begleitendes Dreibein durch eine Drehung in ein anderes Dreibein zu überführen. Nur muß der erste Dreibeinvektor e1(s) im jeweiligen Kurvenpunkt c(s) parallel zur Tangente ![]() gewählt sein.
gewählt sein.
Ein begleitendes Dreibein können wir gut durch seine Ableitungsgleichungen charakterisieren. Diese stellen die Änderungen des begleitenden Dreibeins entlang der Kurve dar. Das Ableitungsgleichungssystem für ein allgemeines Dreibein, was in meiner Arbeit als Verallgemeinerung aller begleitenden Dreibeine gedacht ist, sieht so aus:
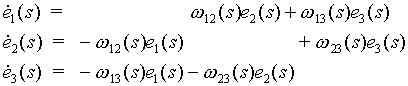
s ist dabei der Bogenlängenparameter und e1(s), e2(s), e3(s) sind die drei Einheitsvektoren des begleitenden Dreibeins.
Die Funktionen ![]() ,
,![]() ,
,![]() heißen verallgemeinerte Krümmungen und sind noch unter den Namen
heißen verallgemeinerte Krümmungen und sind noch unter den Namen ![]() Tangentenkrümmung oder geodätische Krümmung,
Tangentenkrümmung oder geodätische Krümmung, ![]() Normalkrümmung und
Normalkrümmung und ![]() geodätische Windung oder Torsion in der Literatur zu finden. Eine Kurve im Raum ist durch Vorgabe ihrer drei Krümmungsfunktionen, bis auf eine Bewegung, eindeutig bestimmt.
geodätische Windung oder Torsion in der Literatur zu finden. Eine Kurve im Raum ist durch Vorgabe ihrer drei Krümmungsfunktionen, bis auf eine Bewegung, eindeutig bestimmt.
Das klassische Dreibein, worauf die ganze Krümmungstheorie beruht, ist das Frenet-Dreibein, das seine physikalische Bedeutung "natürlich" macht. Als zweiter Dreibeinvektor e2(s) wird der normierte Beschleunigungsvektor ![]() gewählt. Die beiden Vektoren
gewählt. Die beiden Vektoren ![]() ,
, ![]() müssen linear unabhängig sein. Im Vergleich zum allgemeinen Dreibein wird die Krümmung
müssen linear unabhängig sein. Im Vergleich zum allgemeinen Dreibein wird die Krümmung ![]() Null.
Null.
Ein anderes Dreibein, das Pinkall-Dreibein wurde an der TU Berlin in den 80-ger Jahren von Prof. Dr. U. Pinkall entwickelt, um einige graphische Nachteile des Frenet-Dreibeins aufzuheben (Geraden sind keine Frenet-Kurven). Dieses Dreibein wird auch das parallele Dreibein genannt, weil sich es nur in der Bewegungsrichtung verändert, es wird sozusagen in Bewegungsrichtung nur verschoben, und es findet keine Rotation um den Tangentenvektor statt. Anders als zum Frenet-Dreibein, gibt es zu diesem Dreibein keine Konstruktionsvorschrift und keine physikalische Deutung. Im Vergleich zum allgemeinen Dreibein wird hier die Krümmung ![]() (die Torsion) Null. Da zu diesem Dreibein noch wenige theoretische Untersuchungen vorliegen, wollte ich es mit anderen vergleichen.
(die Torsion) Null. Da zu diesem Dreibein noch wenige theoretische Untersuchungen vorliegen, wollte ich es mit anderen vergleichen.
Ein gutes Mittel zum Vergleich der Drehungen verschiedener Dreibeine entlang einer Raumkurve ist der Darboux-Vektor, der nach dem hervorragendem französischem Geometer G. Darboux benannt wurde und dessen Betrag eigentlich die Winkelgeschwindigkeit der Drehung des begleitenden Dreibeins bedeutet. Beim Vergleich von verschiedenen Dreibeinen hat sich ergeben, daß der Darboux-Vektor vom Pinkall-Dreibein den geringsten Betrag hat. Das heißt, daß sich das parallele Dreibein am wenigsten dreht.
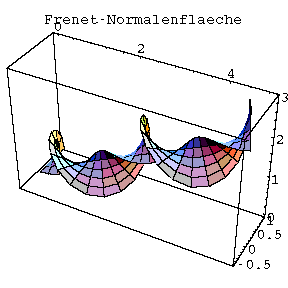
Zwecks besserer graphischer Veranschaulichung der Raumkurven und ihrer unterschiedlichen begleitenden Dreibeine und zwecks ihrer praktischen Anwendung habe ich zwei "raumkurvenbegleitende" Flächen diskutiert (Röhrenfläche und Normalenfläche) und die in der Flächentheorie wichtigen Kenngrößen, wie z.B. die Erste und Zweite Fundamentalform, Weingartenabbildung und Gaußsche Krümmung, berechnet.
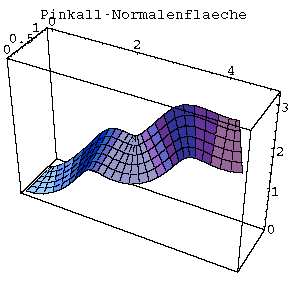
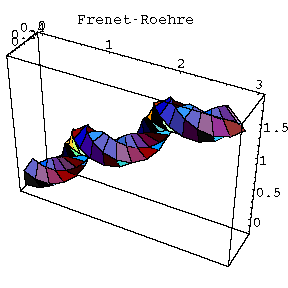
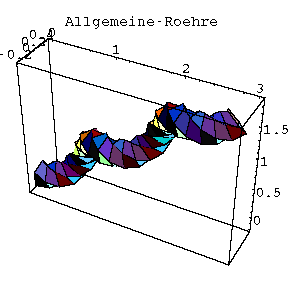
Die Röhrenfläche, die wie ein Gartenschlauch aussieht in dessen Mittelachse die diskutierte Kurve verläuft, eignet sich bestens, um die Unterschiede zwischen verschiedenen begleitenden Dreibeinen graphisch darzustellen. Für diese Zwecke habe ich mit Mathematica die Schraubenlinie mit verschiedenen begleitenden Dreibeinen gezeichnet. Unabhängig davon, mit welchem Dreibein wir zeichnen, bleibt die Kurve und Röhrenfläche mathematisch dieselbe. Es zeigen sich jedoch Unterschiede bei der Zeichnung mit nur einer begrenzten Anzahl von Stützpunkten. Diese Unterschiede sind auf den Bildern gut zu erkennen.
Man sieht, daß die Verdrillungen am wenigstens ausgeprägt sind bei der Pinkall-Röhre, was mit der Tatsache zu tun hat, daß sich das Pinkall-Dreibein am wenigstens dreht, wie schon beim Darboux-Vektor sich gezeigt hat. Das Pinkall-Dreibein wies noch eine interessante Besonderheit auf: Durch Berechnung der Ersten und der Zweiten Fundamentalform hat sich gezeigt, daß bei der Pinkall-Röhre die Parameterlinien die Krümmungslinien sind d.h. die Linien mit den größten bzw. kleinsten Hauptkrümmungen.


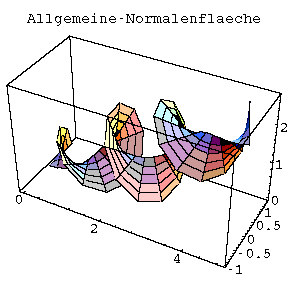
Neben der Röhrenfläche habe ich auch die Normalenfläche studiert, welche zu einer wichtigen Klasse von Flächen, den sogenannten Regelflächen, gehört. Der Name Regelfläche wurde vom französischen surface réglée (geradlinige Fläche) abgeleitet. Man kann sich vorstellen, daß eine solche Fläche gebildet wird durch die Bewegung einer Geraden entlang einer Raumkurve (die auch Leitkurve genannt wird).
Eine Normalenfläche bekommt man, indem man den Normalenvektor ( e2(s) ) eines begleitenden Dreibeins zur Aufspannung der bewegten Geraden verwendet. Je nachdem, was für ein begleitendes Dreibein wir wählen, bekommen wir entsprechend drei verschiedene Flächen: Allgemeine-Normalenfläche, Frenet-Normalenfläche, Pinkall-Normalenfläche (Bild auf der übernächsten Seite).
Nach dem Studium von wichtigen Flächengrößen zeigt sich wieder die gleiche Besonderheit auch bei der Normalenfläche, die am Pinkall-Dreibein ausgerichtet ist. Die Parameterlinien sind auch hier die Krümmungslinien. Diese wiederholte Erkenntnis hat sich als eine Gesetzmäßigkeit beim Pinkall-Dreibein herausgestellt, was in der Arbeit auch bewiesen wurde.
Die Pinkall-Normalenfläche war auch in Hinsicht auf eine andere Flächengröße interessant. Die Gaußsche Krümmung einer Pinkall-Normalenfläche, die ein Maß dafür ist, wie stark sich die Fläche in der Umgebung eines Punktes verbiegt, verschwindet überall, und eine solche Regelfläche, wo die Gaußsche Krümmung überall Null wird, wird in der Literatur eine TORSE genannt.