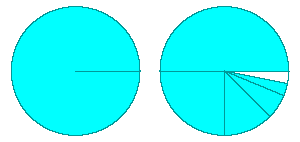
eine ganze Torte und eine halbe Torte und eine viertel Torte und ... . Mit jedem Summanden verringert sich der weiße Teil um die Hälfte. Als Grenzwert ergeben sich zwei Torten.

Die geometrische Reihe
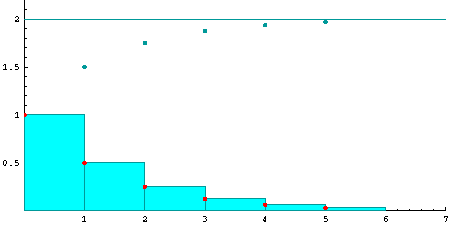
1+ 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + ...
Die Teilsumme der ersten 6 Glieder ist als Flächeninhalt dargestellt:
|
Tortendiagramm:
eine ganze Torte und eine halbe Torte und eine viertel Torte und ... . Mit jedem Summanden verringert sich der weiße Teil um die Hälfte. Als Grenzwert ergeben sich zwei Torten. 
|
Die Glieder der Reihe sind durch rote Punkte und gleichzeitig als Rechteck mit entsprechendem Flächeninhalt dargestellt. Der Wert der Teilsummen (Gesamtinhalt der ersten Rechtecke) wird jeweils durch einen blaugrünen Punkt markiert. Der Grenzwert ist zwei.

|
|
Die harmonische Reihe 1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + ...
Die harmonische Reihe hat keinen Grenzwert, die Teilsummen wachsen über alle Grenzen. Der Flächeninhalt aller Rechtecke ist nicht endlich. |
![[harmon. Reihe]](harm.gif)
|
|
Die alternierende harmonische Reihe 1 - 1/2 + 1/3 - 1/4 + 1/5 - 1/6 + ... .
Die alternierende harmonische Reihe dagegen hat einen Grenzwert (ln2=0.693147). Bei der Bestimmung des Gesamtinhalts der Rechtecke, wird der Inhalt der Rechtecke unterhalb der x-Achse negativ gezählt. |
![[alternierende harmon. Reihe]](altharm.gif)
|
 Weitere Bilder
Weitere Bilder