Prof. Dr. Angela Schwenk

    Taylorpolynome:

    In den folgenden Bildern ist jeweils die Funktion schwarz und ihr Taylorpolynom rot gezeichnet.

  • sin(x)
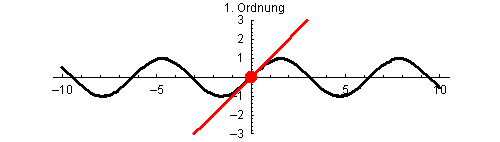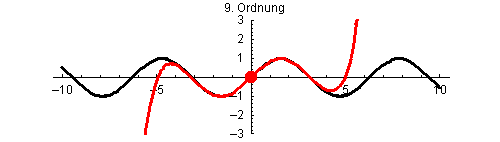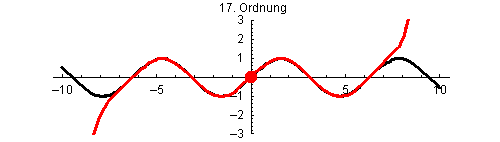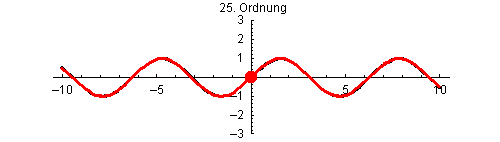    Bei der Funktion sin(x) approximiert das Taylorpolynom mit wachsendem Grad die Funktion immer genauer. Hier werden die Taylorpolynome ungeraden Grades vom 1. Grad p1(x) bis zum 25. Grad p25(x) jeweils mit Entwicklungspunkt x0=0 gezeigt.
    Außerdem ist zu erkennen, wie der Bereich guter Übereinstimmung immer größer wird, was daran liegt, dass der Konvergenzradius R der Taylorreihe von sin(x) unendlich ist.


  • wurzel(x)
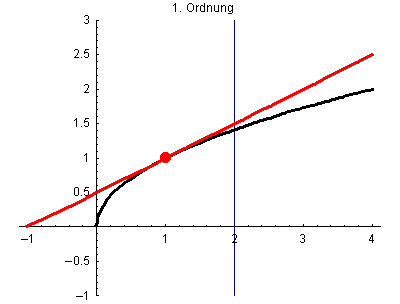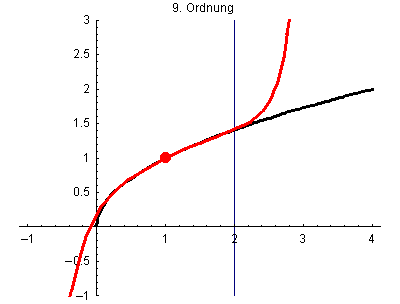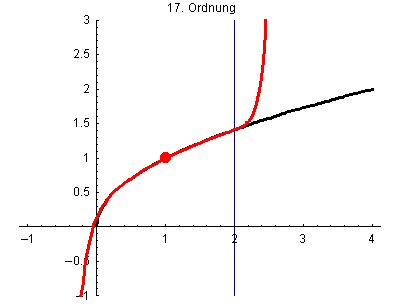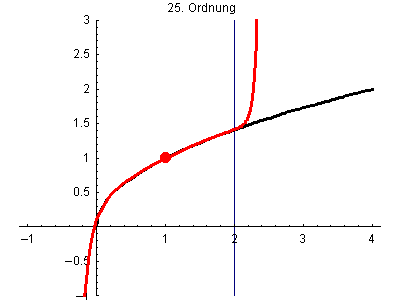    Hier werden die Taylorpolynome 1. Grades p1(x) bis 25.Grades p25(x) von wurzel(x) jeweils mit Entwicklungspunkt x0=1 gezeigt.
    Bei der Funktion wurzel(x) approximiert das Taylorpolynom mit wachsendem Grad die Funktion zwar auch immer genauer, aber der Bereich der guten Übereinstimmung wächst nicht beliebig an, sondern ist auf das Intvervall (0,2) begrenzt. Das liegt daran, dass die Taylorreihe von wurzel(x) mit Entwicklungspunkt x0=1 den Konvergenzradius R=1 hat.

    [zur Idee der Taylorpolynome]


    Pfeil Weitere Bilder

    Letzte Änderung am: 28.06.2013