|
Fourier-Analyse
|
a1sin(w1t), a2sin(w2t)
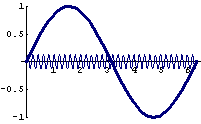
Kennzeichen der Mutterfkt.: unendlich breit (nicht kompakter Träger), Wellen
|
f(t) = a1sin(w1t) + a2sin(w2t)
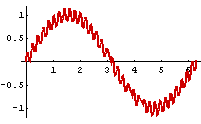
Linearkombination aus verschobenen, gestauchten Versionen einer Grundfkt.
|
Diskretisierte Form
Zeitbereich: {(t, f(t)}t
Frequenzbereich: {( w1, a1), (w2, a2)}
Schneller Algorithmus: FFT (Fast Fourier Transform)
|
|
|
Haar-Wavelet-Analyse
|
Y(t) = 1 für 0<t<½
Y(t) = -1 für ½<t<1
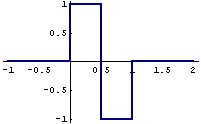
Kennzeichen der Mutterfkt.: endlich breit (kompakter Träger), kleine Wellen
|
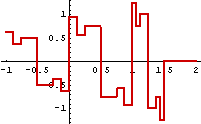
Linearkombination aus verschobenen, gestauchten Versionen einer Grundfkt.
|
Diskretisierte Form
Zeitbereich
Transformationsbereich
Schneller Algorithmus: FWT(Fast Wavelet Transform)
|
|
|
Fourier - Wavelet
|
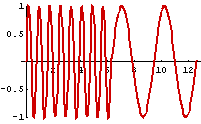
Diskretisierte Form{(t, f(t)}t
w1, w2 aber Wechsel zum Zeitpunkt t0
Fourier-Analyse kann das nicht ad hoc
Wavelets analysieren "gleichzeitig Frequenz w1, w2 und Zeit t0" (Musik)
Geeignet für
Analyse von abrupten Änderungen in den Daten (Meßwerte aus Technik, Wirtschaft und Statistik)
Kompression von Daten
|
|


 Home
Page Mathematik
Home
Page Mathematik  Home
Page TFH
Home
Page TFH
 Home
Page Mathematik
Home
Page Mathematik  Home
Page TFH
Home
Page TFH