Eine einheitliche Darstellung von ebenen, verallgemeinerten Rollbewegungen und deren Anwendungen

Zusammenfassung der Diplomarbeit von Roberta Aust WS2001

Betreuerin: Prof. Dr. Angela Schwenk-Schellschmidt
Gutachter: Prof. Dr. Echter Gerlach

Die Arbeit beschäftigt sich mit der Untersuchung von Bewegungsabläufen zweier Ebenen, die durch Abrollen oder Rollgleiten zweier beliebiger Kurven aneinander, entstehen.
Jede Bewegung läßt sich darstellen als Drehung mit anschließender Translation. Die Multiplikation zweier komplexer Zahlen kann man als Drehstreckung oder Drehstauchung interpretieren. Somit lassen sich ebene Rollbewegungen mit Hilfe der komplexen Zahlen beschreiben. Die Momentanaufnahme der rollenden Kurve kann man als Bild der Kurve unter einer geeigneten Bewegung interpretieren. Die rollende Kurve läßt sich also als Bild unter einer Schar von Bewegungen beschreiben.

Ein Bewegungsablauf einer Ebene E₁E₂ besteht nicht nur aus einer Einzelbewegung, sondern aus einer Schar von Bewegungen. Er wird durch eine lineare Abbildung beschrieben, die jedem tI, I, I Zeitintervall, eine Bewegung E₁E₂ zuordnet.

Jetzt können wir den Bewegungsablauf definieren als:

Wobei die Drehung und T(t) die Translation beschreiben.

Damit die Bewegung stets regulär ist, setzen wir (t) und T(t) als unendlich oft differenzierbar voraus.

Wir betrachten zwei reguläre Parameterkurven g:IE₁, h:IE₂. Damit g während der Bewegung auf h abrollt, müssen bestimmte Voraussetzungen erfüllt sein.

Definition: Rollbewegungen

Eine Schar von Bewegung E₁E₂ wird als Rollbewegung von g auf h bezeichnet, wenn folgende Voraussetzungen erfüllt sind.

1. Der Kurvenpunkt g(t₀) wird t₀I mit der Bewegung zb(t₀,z) auf den Punkt h(t₀) abgebildet.
2. Durch die Abbildung zb(t₀,z) wird die in E₁ liegende Kurve g auf die Kurve tb(t₀,g(t))E₂ abgebildet. Diese Kurve berührt dabei die Kurve h im Punkt h(t₀). Das heißt, die Tangentenvektoren sind parallel.

Die Beträge der Tangentenvektoren unterscheiden sich nur um den Faktor (t0). (t₀) wird als Rollgleitzahl bezeichnet. Für Rollgleitbewegungen sind die Voraussetzungen 1), 2) ausreichend. Für das reine Abrollen wird zusätzlich (t)1 t vorausgesetzt.

Für die Berechnung der Bewegungsgleichung benötigen wir jetzt die Drehbewegung und die Translationsbewegung. Wir erhalten für die Drehung:

und die Translation .

Für Rollbewegungen müssen wir zusätzlich noch voraussetzen, dass sich die entsprechenden Punkte auf Ihrem jeweiligen Kurvenstück gleich schnell bewegen, also |h'(t)|=|g'(t)|. Damit vereinfachen sich die Gleichungen zu:

,  .

Beispiele für Rollbewegungen

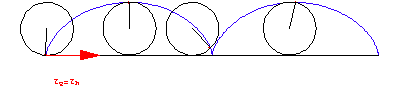
Außenrollung (Epitrochoide)	Innenrollung (Hypotrochoide)
Abb. 1: Rollkurven von Kreisen in bzw. auf Kreisen

Abbildung 1 zeigt einige durch Rollbewegungen entstandene Rollkurven und die Momentanbilder der rollenden Kurven. Die rollende und die feste Kurve haben die gleichen Tangentenvektoren, (t)1.

Eine weitere interessante Anwendung von Rollgleitbewegungen ist die Konstruktion der entsprechenden Kurven bei gegebener Bewegungsgleichung und gegebener Rollgleitzahl. Um die Bewegung unter Kontrolle zu behalten, wählen wir 1, aber konstant.

Zu einem gegebenen Bewegungsablauf b:IE₁E₂ und gegebener Rollgleitzahl lassen sich dann reguläre Parameterkurven g, h konstruieren, für die gilt, g gleitet unter b auf h ab.

Vor.: '(t)0
Geg.: b, (t)1
Ges.: g, h
Nach der Definition einer Rollbewegung gilt: h(t)=b(t,g(t))=g'(t)-T(t)       (1)
Die Drehung ist gegeben durch:     (2)

Durch Ableitung der Gleichung (1) und anschließendem Gleichsetzen mit Gleichung (2) erhalten wir schließlich eine lineare Differentialgleichung 1. Ordnung für die rollende Kurve g.

Wir gehen von dem Bewegungsablauf b aus, der das Abrollen von Kreisen auf bzw. in Kreisen beschreibt und als Rollkurven die Trochoiden liefert (siehe Abb. 1). Mit der DGL (3) lassen sich nun zwei Kurven g und h finden, die unter b mit konstanter Rollgleitzahl aneinander rollgleiten.

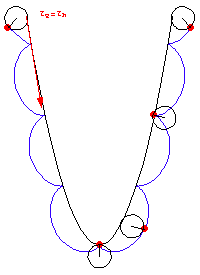
Gehört der gegebene Bewegungsablauf zur Außenrollung, so sind die konstruierten Kurven stets Trochoiden. Ist die rollende Kurve eine Epitrochoide (Außenrollung), so ist die feste Kurve eine Hypotrochoide und umgekehrt (siehe Abb. 2).

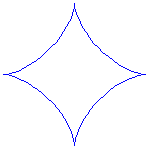
Abb. 2: rollende und feste Kurve bei der Außenrollung

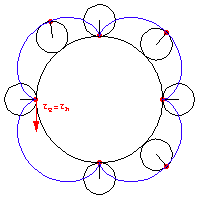
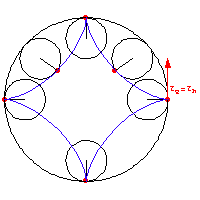
Gehört der gegebene Bewegungsablauf b zur Innenrollung, entstehen ebenfalls Trochoiden. Hier gehören aber die entstehenden Kurven einer Trochoidenart an. Entweder sind beide Kurven Epitrochoiden oder beide Kurven sind Hypotrochoiden (siehe Abb.3).

Abb. 3: rollende und feste Kurve bei der Innenrollung

Die Konstruktion der Kurven bei der Außenrollung findet eine Anwendung in der Zykloidenverzahnung. Bei dieser Verzahnungsart werden die Kopfflanken von Teilen von Epizykloiden und die Fußflanken von Teilen von Hypozykloiden gebildet.

Weitere Anwendungen von Rollbewegungen sind z.B. der Wankelmotor, die Brachistochrone und das Zykloidenpendel.

Letzte Änderung am: 09.02.2002 von Angela Schwenk