Beschreibung und Erzeugung von Minimalflächen
Zusammenfassung der Diplomarbeit von René Heidenreich SS 2006 E-Mail: ![]()
Betreuerin:
Prof. Dr. Angela Schwenk-Schellschmidt
Gutachterin: Prof. Dr. Margitta Pries
In dieser Arbeit geht es um, wie der Titel schon sagt, Minimalflächen. Was ist aber nun eine Minimalfläche? Anschaulich gesehen handelt sich es dabei um eine Fläche die gegenüber anderen Flächen, mit gleicher Randkurve, den kleinsten Flächeninhalt besitzen.
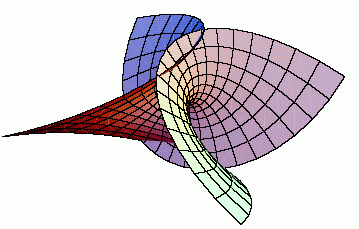
Abbildung 1: Enneper-Fläche |
Seit den sechziger Jahren werden sie als Modelle für leichte Dachkonstruktionen eingesetzt. So stellt zum Beispiel das Dach des Olympiastadions in München, dass 75.000 m2 überdeckt eine Minimalfläche dar. Es sind meistens Zeltdächer, wobei die tragende Konstruktion aus einem Seilnetz besteht. Das Netz wird mit einer dünnen Membran verbunden. Da die Seile vorgespannt werden, benötigt das Dach in sich keine Steifigkeit. Spannt man die Seile so, dass an jedem Seilende die gleiche Kraft auftritt, so erhält man eine Minimalfläche. Die Minimalfläche weist in jedem Punkt eine konstante Spannung in alle Richtungen auf.
Sie treten auch in der Elastizitätstheorie, der Strömungslehre und in allen Gebieten in denen Kapillarkräfte eine Rolle spielen auf. Sie geben oft die optimale Lösung eines Problems.
Eine Minimalfläche ist eine Extremale und für Extremwerte muss bekanntlich die erste Ableitung gleich Null sein. Wenn man dieses Wissen auf Flächen angewendet, gelangt man dazu, dass eine Fläche genau dann einen stationären Flächeninhalt besitzt, wenn ihre mittlere Krümmung identisch verschwindet. So werden seit Lagrange alle Flächen deren mittlere Krümmung H gleich Null ist als Minimalflächen bezeichnet.
Eine Funktion die komplex differenzierbar ist, heißt analytisch. Jede Fläche kann man lokal isotherm parametrisieren. Eine Fläche φ ist genau dann isotherm parametrisiert, wenn
Das trifft genau auf harmonische Funktionen zu. Da der Imaginär- und Realteil komplexer analytischer Funktionen harmonisch ist, geht man zu diesen über. Also man sucht sich eine analytische Funktion und nimmt dessen Real- oder Imaginärteil und stellt zusätzlich noch sicher, dass die isotherme Bedingung erfüllt ist und erhält eine Minimalfläche.
Die Enneper-Weierstraß-Darstellung einer Minimalfläche lautet:
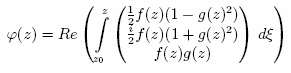 .
.Mit f, g als zwei beliebige analytische komplexe Funktionen und z=u+iv stellt φ(z) die Parametrisierung einer Minimalfläche dar. Durch z0 verschiebt sich die Fläche nur im Raum. Bei Wahl von verschiedenen Funktionen erzeugt man seine eigenen Minimalflächen. Dass diese dann isotherm sind stellt die arithmetische Form der Funktion im Integral sicher. Durch das Integral entsteht eine analytische Funktion.
So berechnet sich die Enneper Minimalfläche aus f=2, g=z und die Helikoide durch f=ie-z, g=e-z.
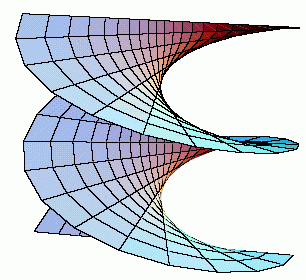
Abbildung 2: Helikoide |
Als problematisch stellt sich dabei manchmal heraus, dass das Integral schwer lösbar ist. Dadurch, dass es unendlich viele Parametrisierungen gibt, existieren auch sehr komplizierte Lösungen für ein und dieselben Fläche. Aber durch eine geschickte Wahl der Funktionen, entsteht eine Integral freie Darstellung.
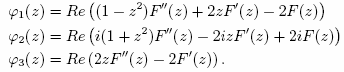
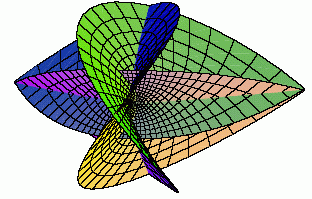
Abbildung 3: Fläche, die sich für F=cos(z) ergibt. |
Die Arbeit geht noch auf ein anderes Problem ein. Das Plateau´sche Problem wurde erstmals von J.L.Lagrange (1736-1813) im Jahre 1760 gestellt. Es ist die Aufgabe, zu einer doppelpunktfreien Kurve eine Fläche mit minimalem Flächeninhalt zu bestimmen, die die Kurve als Rand hat.
Das Problem wurde aber nach dem Physiker J.A.F.Plateau (1801-1883) benannt, der es durch ausführliche Seifenblasenexperimente populär werden ließ. Es trotzte lange Zeit den Bemühungen vieler Mathematiker. Zunächst konnte nur für sehr spezielle Polygonkurven eine Lösung angegeben werden. Die Ersten, die ein Teil des Problems lösen konnten waren J.Douglas und T.Rado.
Plateau zeigte erstmals, dass sich Minimalflächen physikalisch realisieren lassen, wenn man die Randkurve aus Draht nachbildet und diesen in Seifenlauge eintaucht, so nimmt die Seifenblase die Form einer Minimalfläche an. Der Grund dafür liegt in der Oberflächenspannung sowie dem Prinzip der minimalen potentiellen Energie, wenn man die Gravitationskraft vernachlässigt, was wegen der geringen Masse möglich ist.
Es wird unter anderem der Beweis dazu geführt, dass zu jeder einfach geschlossenen Kurve eine Minimalfläche existiert deren Rand die vorgegebene Kurve ist.
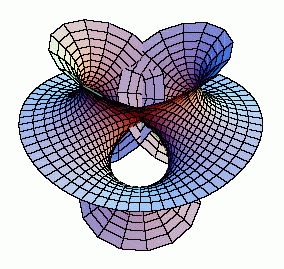
Abbildung 4: Costa Fläche |
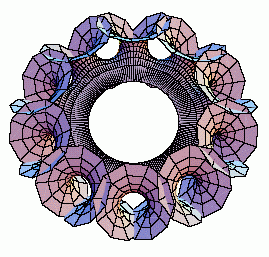
Abbildung 5: Blumenfläche |
Lässt man einen Graphen um die x-Achse Rotieren so entsteht eine Rotationsfläche, die zwischen zwei gegebenen Kreisringen eingespannt ist. Die Rotationsminimalfläche stellt ein Sonderfall des Plateau´schen Problems dar, denn man kann sie direkt, durch dass minimieren des Flächenfunktionals berechnen. Das Funktional
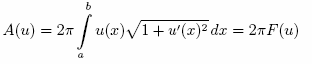
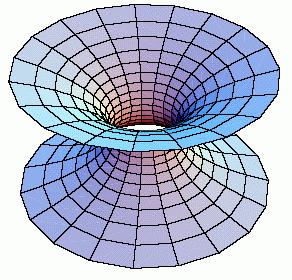
Abbildung 6: Katenoid |
Literatur zu diesem Thema:
- Differentialgeometrie und Minimalflächen von Jürgen Jost
- Für Studenten geeignet und bietet ein kurzes aber verständlich und schlüssiges Werk über die Theorie von Minimalflächen.
- Differentialgeometrie von Alfred Gray
- Ist sehr preiswert und beinhaltet neben einem umfangreichen Wissen über Differentialgeometrie, schöne Verbindung zu Mathematica von der selbst der erfahrenere Mathematica-Nutzer profitiert.
- Minimal Surfaces I
- aus den Grundlehren der mathematischen Wissenschaften 295
Ist in Englisch und für jemanden der schon ein Grundwissen besitzt. Aber es beinhaltet nahezu alles zum Thema Minimalflächen. Aufgrund des hohen Preises ca. 65 Euro nur zum Ausleihen geeignet. Wer sich ernsthaft mit Minimalflächen beschäftigt kommt an diesem Buch nicht vorbei.