Result. Math. 52 (2008) 369-384
Angela Schwenk
Pedal curves
Part I: homogeneous differential equation
In the following are some illustrations referring to the article.
1 Introduction
Second Equivalence Theorem / 3. Examples
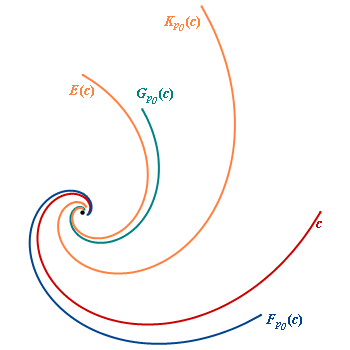 If the curve is a logaritmic spiral and p0 is the center of the spiral, then each derived curve of c like the Evolute E(c), the pedal curve FP0(c), the co-pedal curve Gp0(c) and the caustic Kp0(c) all with respect to p0, is also a logarithmic spiral with the same progression as c and center p0.
If the curve is a logaritmic spiral and p0 is the center of the spiral, then each derived curve of c like the Evolute E(c), the pedal curve FP0(c), the co-pedal curve Gp0(c) and the caustic Kp0(c) all with respect to p0, is also a logarithmic spiral with the same progression as c and center p0.
Vice versa, the property that each of the derived curves can be obtained from c by a rotation togehter with a homothety wrt. p0 characterises logarithmic spirals.
2. Preliminaries
2.1. Spherical parametrization
Illustrations of the spherical parametrization
2.3. The pedal and co-pedal curve
For a given regular curve c and a given point p0 we consider the foot Fp0(c) of the
perpendicular from p0 to the tangent of c and the foot Gp0(c) to the normal of c.
The curve traced out by Fp0(c) is called pedal curve of c with respect to p0; we call the curve traced out by Gp0(c) co-pedal curve of c.

Logarithmic spiral (red), the point p0 defining the pedal F and the co-pedal G is the center of the spiral. |
It is a characteristic property of a logarithmic spiral, that all rectangles, built by both foot points, the curve point and by the center p0 of the spiral, moving along the curve are proportional.
[Animation].
The rectangles moving along the curve have changing shapes, choosing another point p0 or a another curve c.
2.5. The caustic
We consider a point p0 as a center of light and a regular curve c with
p0 not beeing in the trace(c) as a shape of a mirror. The envelope of the reflected rays is called
the caustic Kp0(c) of c with respect to p0.

The center of light is the center of a logarithmic spiral. The caustic K is also a logarithmic spiral. |
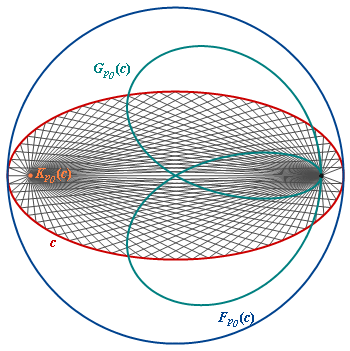
Special situation: The center of light is one focus of an ellipse (red), the caustic K is degenerated to the second focus. The pedal F wrt a focus is a circle. |
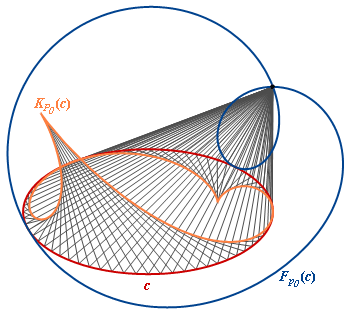
Reflection by an ellipse, the center of light is outside the ellipse. |
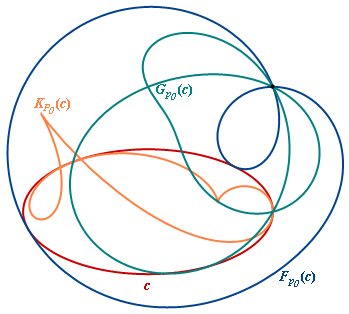
An ellipse and its caustic K, its pedal F and its co-pedal G all wrt p0 outside the ellipse. |