Prof. Dr. Angela Schwenk

  Schnitte durch den Graphen der Funktion z=f(x,y)=x²-y²

y=konstant: Schnitt parallel zur z-x-Ebene

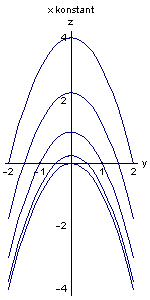
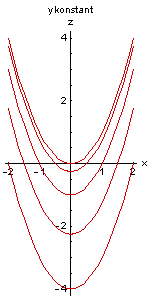
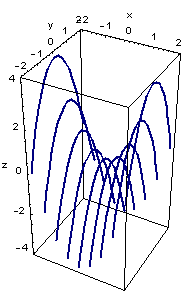
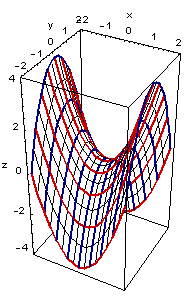
Eine Art, die Funktion systematisch zu untersuchen, besteht darin, eine der Variablen als Konstante zu betrachten, und dann die Funktion als Funktion der verbleibenden Variablen zu diskutieren. In der linken Abbildung sind die Funktionen z=f(x,y0)=x2-y02 für die Werte y0=0, y0=±0.5, y0=±1, y0=±1.5 und y0=±2 gezeichnet. Es ergeben sich hier um y02 nach unten verschobene Normalparabeln. In der E-Technik ist diese Darstellung von den Kennliniendiagrammen bekannt. 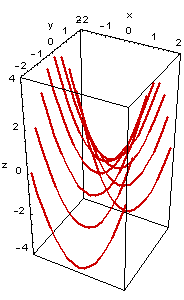In der rechten Abbildung sind diese Kurven als Raumkurven mit den jeweils entsprechenden y-Werten gezeichnet.

x=konstant: Schnitt parallel zur z-y-Ebene

Hier ist jeweils x konstant. In der linken Abbildung sind die Funktionen z=f(x0,y)=x02-y2 für die Werte x0=0, x0=±0.5, x0=±1, x0=±1.5 und x0=±2 gezeichnet. Es ergeben sich diesmal nach unten geöffnete um x02 nach oben verschobene Parabeln. In der rechten Abbildung sind diese Kurven als Raumkurven mit den jeweils entsprechenden x-Werten gezeichnet.

Graph der Funktion

Die räumlichen Schnittkurven ergeben zusammen den Graphen der Funktion.

z=konstant: Schnitt parallel zur x-y-Ebene

Die Projektionen der Schnittlinien z=konstant auf die x-y-Ebene ergeben genau die Höhenlinien. Klicken Sie hier für eine Animation.

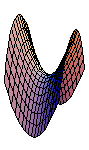
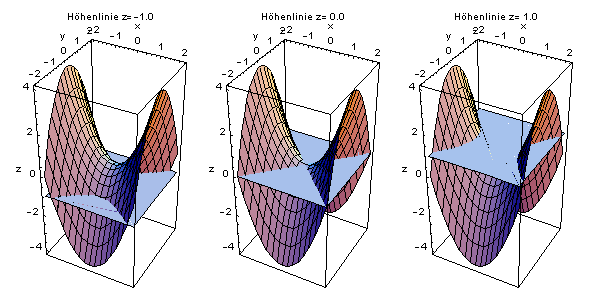
Wertetabelle, Höhenliniendiagramm

Weitere Bilder

Letzte Änderung am: 21.05.2014