
Mit der Abbildung f(z)=1/z wird jedem Punkt z der komplexen Ebene der Punkt w=1/z zugeordnet.
In den folgenden Bildern ist jeweils links die "z-Ebene" und rechts die "w-Ebene" gezeichnet.
Kurven gleicher Farbe werden aufeinander abgebildet. Dabei kann man gut beobachten, wie die Abbildung f(z)=1/z Punkte, die dicht am Ursprung liegen, auf Punkte abbildet, die weit weg vom Urspung sind, bei gleichzeitiger Spiegelung an der reellen Achse.
Die Abbildung f(z)=1/z hat die Eigenschaft, daß Geraden und Kreise wieder in Geraden oder Kreise abgebildet werden.
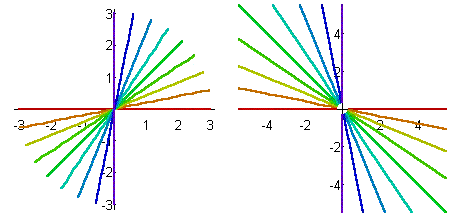
Geraden durch den Ursprung werden wieder in Geraden durch den Ursprung abgebildet:

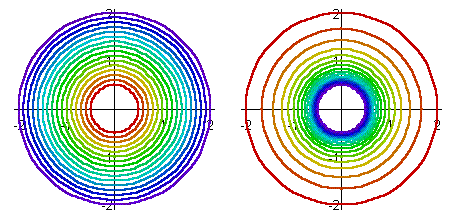
Kreise mit Mittelpunkt im Ursprung werden wieder in Kreise mit Mittelpunkt im Ursprung abgebildet:
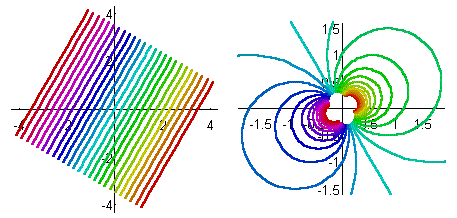
Geraden, die nicht durch den Ursprung gehen, werden in Kreise abgebildet, die durch den Ursprung gehen:
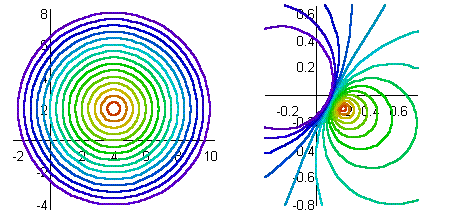
Beliebige Kreise (die den Mittelpunkt nicht im Ursprung haben und die nicht durch den Ursprung gehen) werden wieder in beliebige Kreise abgebildet:
 Weitere Bilder
Weitere Bilder