
 |
 | |
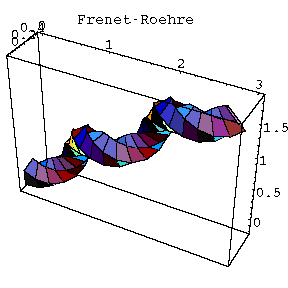
| Bei der Frenet-Röhre ist eine Kante durch den Hauptnormalenvektor der Kurve (zweiter Vektor des Frenet-Beins) bestimmt. Die Röhrenfläche erscheint verdrillt, die Querschnittsfläche wird dabei verdreht. Die Änderungsrate des Drehwinkels der Querschnittsfläche ist gerade die Torsion einer Raumkurve. | Bei der Pinkall-Röhre dagegen ist die Querschnittsfläche parallel längs der Kurve verschoben, die Kanten stehen stets senkrecht auf der Querschnittsfläche. |
 Weitere Bilder
Weitere Bilder
 Home Page Mathematik
Home Page Mathematik