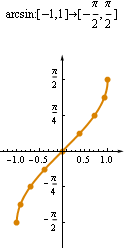Prof. Dr. Angela Schwenk
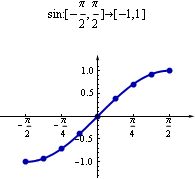
Umkehrfunktion der Sinus-FunktionBeschränkt man sich auf den umrahmten Teil der Wertetabelle (siehe Tabelle 1), dann kann auch die umgekehrte Tabelle als Wertetabelle einer Funktion aufgesfasst werden. Das ist dann die Wertetabelle der sogenannten Umkehrfunktion. In Tabelle 2 ist der Ausschnitt von oben noch einmal dargestellt. Der rechte, orange Teil ist die Wertetabelle der Arcsin-Funktion. Der eingeschränkte Definitionsbereich, so dass die Sinus-Funktion f umkehrbar ist, ist das Intervall Bei der Umkehrfunktion f -1 ist das genau umgekehrt: Definitionsbereich Abbildung 2 zeigt die zugehörigen Graphen. Achtung: missverständliche SchreibweiseDie Umkehrfunktion wird in der Mathematik durch eine hochgestellte "-1" gekennzeichnet. Diese hochgestellte "-1" hat in der Mathematik also zwei Bedeutungen, die nicht verwechselt werden dürfen und die nichts miteinander zu tun haben:
So wird auf dem Taschenrechner die Umkehrfunktion der Sinusfunktion häufig mit |
|
||||||
 Weitere Bilder
Weitere Bilder

 Tabelle 1: Wertetabelle und umgekehrte Wertetabelle
Tabelle 1: Wertetabelle und umgekehrte Wertetabelle