Abb. 1
|
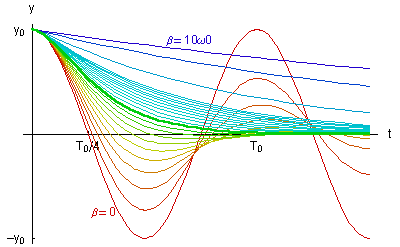
Abbildung 1 zeigt die Auslenkungen y(t) eines schwingenden Körpers als Funktion der Zeit für verschiedene Dämpfungen Die Dämpfung variiert von Der aperiodische Grenzfall Klicken Sie hier, zur Animation der einzelnen Kurven. |
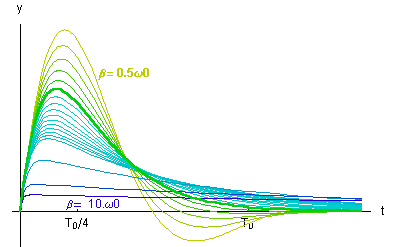
Abb. 2
|
Für Abbildung 2 wird der schwingende Körper am Anfang aus der Ruhelage angestoßen Die Dämpfung variiert von Der aperiodische Grenzfall Klicken Sie hier, zur Animation der einzelnen Kurven. |
Die Lösungen der homogenen Schwingungsgleichung spielen für den Einschwingvorgang bei erzwungenen Schwingungen eine Rolle.
 Schwingungsgleichungen - Übersicht
Schwingungsgleichungen - Übersicht
 Weitere Bilder
Weitere Bilder
 Home Page Mathematik
Home Page Mathematik