Die Abbildungen unten zeigen die Lösungen der inhomogenen DGL bei gleicher ![]()
![]()
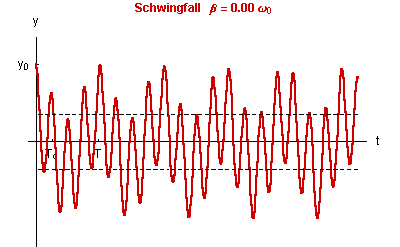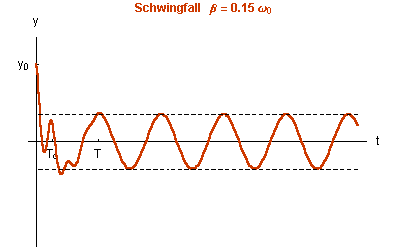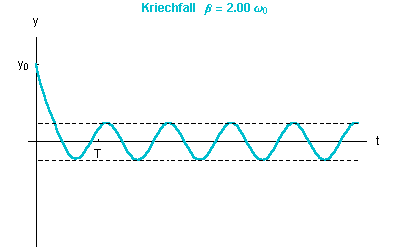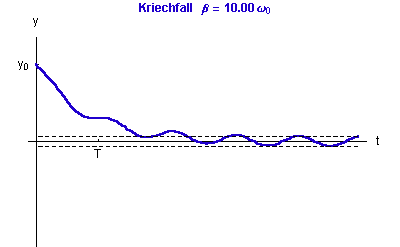 |
Die Dämpfung bestimmt die Abklinggeschwindigkeit der homogenen Lösung und damit die Dauer des Einschwingvorganges.
Im ungedämpften Fall Man kann beobachten, wie die Amplitude der stationären Schwingung mit wachsender Dämpfung |
 Schwingungsgleichungen - Übersicht
Schwingungsgleichungen - Übersicht
 Weitere Bilder
Weitere Bilder
 Home Page Mathematik
Home Page Mathematik