|
Wavelets in Kürze
Zielgruppe / Voraussetzungen:
MathematikstudentenInnen ab dem 6. Semester / Fähigkeit, mathematisch zu denken, speziell Grundkenntnisse mit dem Computeralgebraprogramm Mathematica, der Matrizenrechnung, im letzten Viertel von Vektorräumen (Funktionenräumen), Konvergenz von Funktionsreihen.
Zielsetzung:
Die Veranstaltung gibt für den mathematischen
Normalverbraucher eine Annäherung an das aktuelle Thema Wavelets,
die neuartige Systeme von Basisfunktionen sind. Hauptanwendungsgebiete
sind die Signalverarbeitung und Bildverarbeitung. Unter Verarbeitung wird
hier die Analyse, "Reinigung", Filterung, rationelle Speicherung und Übermittlung
von Zeitsignalen bzw. Bilddaten sowie vor allem deren Verdichtung verstanden.
Unterrichtsmethode:
Die Veranstaltung orientiert sich an dem Buch von Yves Nievergelt: Wavelets Made Easy, Birkhäuser Verlag 1999, DM 88,50. In den Übungen wird die Theorie mit dem Wavelet Explorer von Mathematica anschaulich und experimentell erschlossen. Für den ersten Teil der Vorlesung liegt ein Skript vor.
Inhalt:
Es werden folgende Fragen beantwortet: Was sind Wavelets? Wavelets erweitern die Fourier Analyse. Wie werden Wavelets berechnet? Es gibt schnelle Algorithmen. Die Lehrveranstaltung beginnt mit einer elementaren, jedoch exakten Einführung in die Natur der mathematischen Wavelets (Alfred Haar’s Wavelet). Zwei erste Demonstrationsbeispiele sind eine Analyse der Wassertemperatur eines Flusses und der Börsenkurse. Dann werden zweidimensionale Wavelets präsentiert. Weitere Demonstrationsbeispiele sind Lärmreduktion (Rauschen), Datenkompression (mit wenig Verlusten) und Entdecken von Sprüngen in einem Datenstrom. Die algebraische Struktur der Wavelets wird am Beispiel von Ingrid Daubechies‘ Wavelet behandelt. Im letzten Viertel der Lehrveranstaltung wird der mathematische Kontext behandelt, in dem Wavelets entstanden sind: Fourier Analyse von Signalen und Funktionen.
|
Beispiel: Das akustische Signal
des Worts
Mathematica sieht so aus:
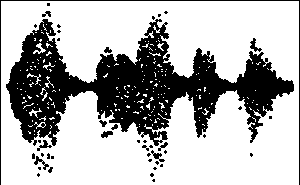
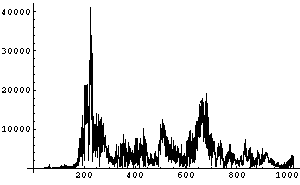
Die Fourier-Transformation ergibt die Fourier-
Koeffizienten über den Frequenzbereich
(1-dimensional):
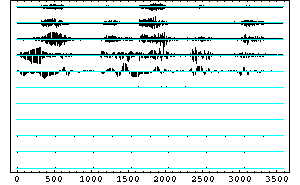
Die Wavelet-Transformation ergibt die Wavelet-
Koeffizienten über den Zeitbereich zu allen
Frequenzniveaus, die vertikal aufgetragen sind
(2-dimensional):
|



 Home
Page Mathematik
Home
Page Mathematik  Home
Page TFH
Home
Page TFH
