Prof. Dr. Angela Schwenk

Die erzwungene Schwingung - Resonanz

Die erzwungene Schwingung wird durch die inhomogene Schwingungsgleichung    y" + 2betay ' + omega02 y = F0cos(omegat)    beschrieben.
Die erzwungene Schwingung ist eine Überlagerung einer Lösung der zugehörigen homogenen Gleichung (abklingende freie Schwingung) mit der partikulären Lösung der inhomogenen Gleichung (stationärer Anteil). Der homogene Lösungsanteil bestimmt den Einschwingvorgang. Der stationäre Anteil ist eine harmonische Schwingung, deren Kreisfrequenz mit der Erregerkreisfrequenz omega übereinstimmt und deren Amplitude von der Erregerfrequenz und der Dämpfung beta abhängt.

Die Graphiken in Abb. 1 zeigen die Lösungen der inhomogenen DGL bei gleicher Dämpfung beta= 0.1 omega0 aber für verschiedene Erregerkreisfrequenzen omega:


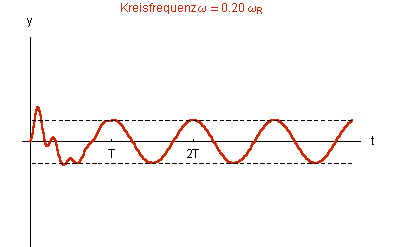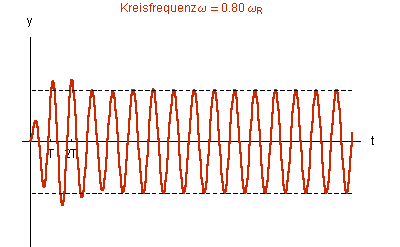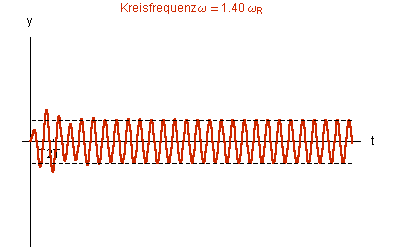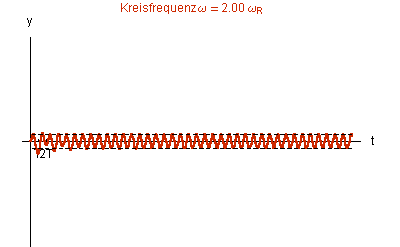
Abb. 1 		Bei wachsender Erregerkreisfrequenz omega wächst die Amplitude an, um dann wieder abzunehmen. Die Kreisfrequenz, die die größte Amplitude bewirkt, heißt Resonanzkreisfrequenz omegaR.

Da die Dämpfung beta hier nicht verändert wird, zeigen alle Lösungen ein gleich langes Einschwingverhalten.


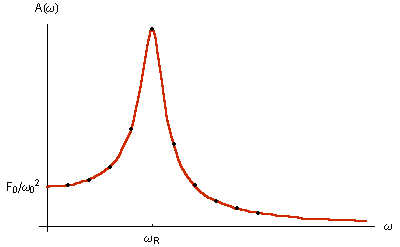
Abbildung 2 zeigt die Abhängigkeit der Amplitude von der Erreger(kreis)frequenz bei der fest gewählten Dämpfung beta= 0.1 omega0 als sogenannte Resonanzkurve. Die Frequenzen aus Abb. 1 sind markiert. Die Kurve hat bei der Resonanzfrequenz ihr Maximum.
Abb. 2

[Resonanzkurven im Vergleich]
 <- Schwingungsgleichungen - Übersicht             <- Weitere Bilder      <- Home Page Mathematik

Letzte Änderung am: 01.04.2009