Was ist Differentialgeometrie?
Aus Sicht des Anwenders liefert die Differentialgeometrie u.a. Antworten zu folgenden Fragestellungen:
- Wie verbinden Straßenbauer ein gerades Straßenstück mit einem Kreisbogen, so dass die Bahn ohne abrupte Lenkbewegungen befahren werden kann?
- Welche Kräfte wirken auf einen Körper, der sich auf einer vorgebenen Bahnkurve bewegt?
- Welche Verbindung ist die kürzeste von Berlin nach New York, wenn man die Erde als Kugel idealisiert?
- Wodurch sind Flächen mit kleinster Oberfläche (Minimalflächen, Seifenblasen) ausgezeichnet?
- Wie reflektieren krumme Spiegel?
- Wie wird die Beleuchtung eines Körpers im Computer simuliert?

Aus Sicht des Studenten ist die Differentialgeometrie ein Fach,
- das Fächer aus dem Mathematik-Grundstudium eng verbindet, besonders Analysis und Lineare Algebra,
- das den Begriff der Funktionalmatrix anschaulich neu beleuchtet,
- dessen Inhalte z.B. mit Mathematica sichtbar gemacht werden können.
Aus Sicht des Mathematikers behandelt die Differentialgeometrie Kurven und Flächen. Eine wesentliche geometrische Größe, mit der Kurven und Flächen beschrieben werden, ist die Krümmung:
- Kurven in der Ebene:
- Flächen im Raum
|
Was ist die Krümmung Beispiel: Ein Kreis vom Radius r ( x(t)=rcos(t), y(t)=rsin(t) ) hat konstante Krümmung |
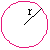 |
|
Im Allgemeinen ist die Krümmung Zusammen mit der Bogenlängenfunktion s (sie entspricht der Angabe des "Tageskilometerzählers" im Auto) bestimmt die Krümmungsfunktion |
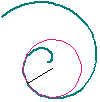 |
|
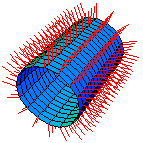
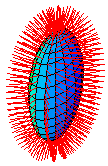
Der Krümmungsbegriff für Flächen ist vielschichtiger als der für Kurven. Wie das Beispiel eines Zylinders zeigt, hängt die Krümmung einer Fläche auch von der Richtung ab. Wird in jedem Punkt der Fläche ein Einheitsvektor gezeichnet, der senkrecht auf der Tangentialebene steht, verwandelt sich der Zylinder durch das so entstandene Normalenfeld in einen "Lockenwickler". Die Krümmung einer Fläche wird durch die Änderung des Normalenfeldes beschrieben. Die Krümmung ist dort groß, wo sich die Normalenvektoren stark "spreizen". Seifenhäute sind Minimalflächen; in jedem Punkt verschwindet der Mittelwert der größten und kleinsten Krümmung. Beispiele sind Katenoid und Helikoid. Weitere Beispiele zur Differentialgeometrie.
|
|